Y-Wing (XY-Wing) Sudoku Strategy

The XY-Wing which is also called the Y-Wing is a good Sudoku strategy that can help solve advanced Sudoku puzzles when you are stuck.

The XY-Wing is a part of the “Wing” family of strategies and therefore uses patterns common with this family of strategies. This means that learning the XY-Wing can help you with other solving strategies such as the W-Wing and XYW-Wing.

Here is the simplest explanation of the XY-Wing strategy:

An XY-Wing is made up of three bi-value cells. One of these bi-value cells is known as the pincer which shares the same house as the other two bi-value cells known as the wings.

Each candidate in the pincer will match one candidate in each of the wings. The other candidates in the wings will be the same between both wings.

If this technical explanation was enough, play a real Sudoku game and try spotting a XY-Wing. If not, don’t worry we have an in depth explanation with examples.

How to spot an XY-Wing strategy:

Between the three bi-value cells there will be three common candidates, let’s refer to them as A, B and C. If the pincer or the cell that shares the same house as the wings has candidates AB then one of the wings will have candidates AC and the other wing candidates BC. This will allow the wings to connect to the pincer through weak links.

Let’s take a look at an example:

The red shaded square in r6c7 is a bi-value square that contains two candidates (4 & 8) which we can refer to as (A & B). This means that we need to find two other bi-value cells that share the same house, while connecting to one of the candidates in the pincer (A & B) while also sharing a common third candidate between the two wings.

The two cells that will act as the wings are shaded in blue. The first wing is in r2c7 and contains the candidates (2 & 4). Since the four in the pincer is referred to as A, we will also call this A in the wing and the other candidate which is a two will be referred to as C. This cell is known as (C & A) and connects to the pincer through A which creates a weak link.

The second blue shaded square in r4c9 has (2 & 8) since we have already declared these numbers this shaded square will be (C & B) and it connects to the pincer through B as they both share the candidate 8.

We can also make the connection that these two wings also share a common candidate with each other. This candidate is the 2 which is the C. Since this example follows the rules we laid out, we can confirm that it is a valid XY Wing.

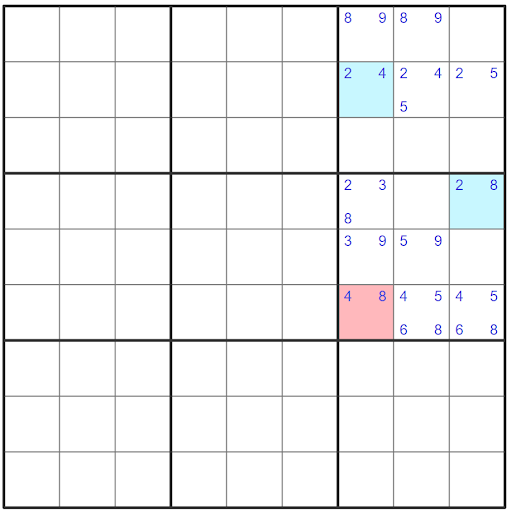
Since this is a valid XY-wing we can eliminate some candidates that will help us in solving this puzzle. As we determined earlier an XY-wing is a Type 1 alternate inference change which means that one of the ends will be false and the other true.

We can see this as the link within the bi-value cells are strong links and the three cells are connected through weak links. This follows the pattern of an AIC type 1 which has an odd number of connections and both starts and ends on a strong link.

The black arrows show the strong links which are:

Between the 2 & 4 in cell r2c7 Between the 4 & 8 in cell r6c7 Between the 2 & 8 in cell r4c9

The red arrows show the weak links which are: Between the 4’s in cell r2c7 and r6c7 Between the 8’s in cell r6c7 and r4c9

Since this chain ends and start with strong linked vi-value cells, we have a Type 1 AIC which means that one of the ends of the chain has to be true.

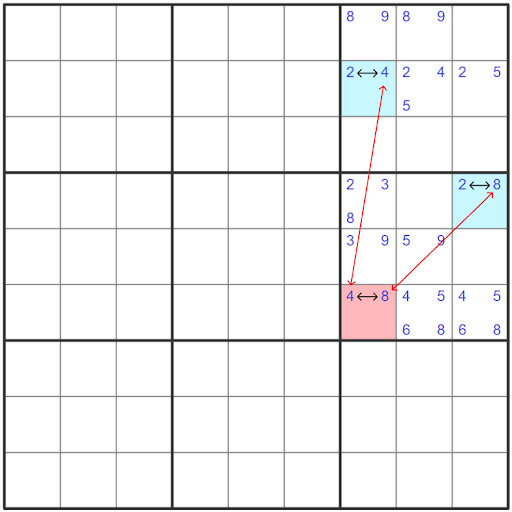
Since one end of the chain has to be true, that means that the other will be false. However, this means that we can eliminate all of the candidates in the cells where these wings can see each other or are in the same house. This follows the logic that if one of these cells is true, then it would not be possible for the other to be true where they can see each other.

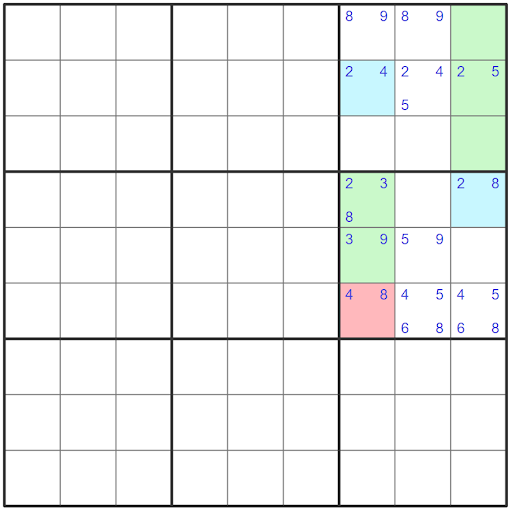
Highlighted green are the areas where both wings see each other as they are a part of the same house which means that candidate C can be eliminated. Note that the pincer is not highlighted green even though it intersects with both wings. For a valid XY-wing the pincer will never contain candidate C that both the wings share.

XY-Wing example

Let’s go through another example of an XY-wing with more numbers filled in to show how this pattern may appear in a Sudoku puzzle.

To spot the XY-Wing pattern we need to start looking for three bi-value cells with three common candidates. We can see from the puzzle below that there is an XY-Wing with the cells shaded in blue acting as the wings and the red shaded cell acting as the pincer.

For this to be a valid XY-Wing the pincer has to see both of the wings and will have each of its candidates connect to one in each of the wings. Both wings then have to share the other common candidate that is not creating the weak link to the pincer. We can confirm this as the following is true.

The pincer sees the wing in r8c4 as they share the same block The pincer sees the wing in r1c4 as they share the same column The pincer has a weak link with cell r8c4 through candidate 1 The pincer has a weak link with cell r1c6 through candidate 8 The wings share common candidate 7

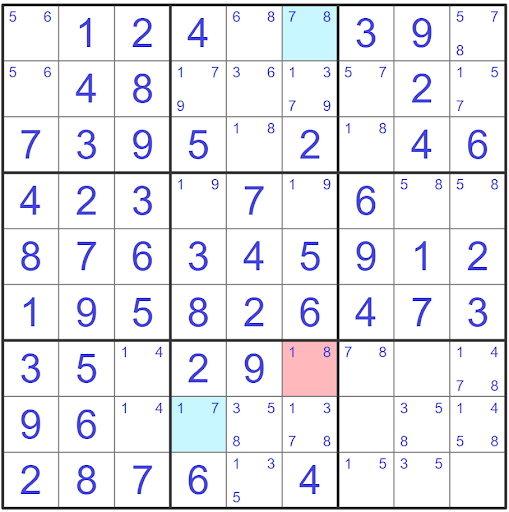
Since this example has been determined to be a valid XY-Wing we are able to remove the common candidate which is 8 from cells where both of the wings share the same house. These cells are highlighted in green below.

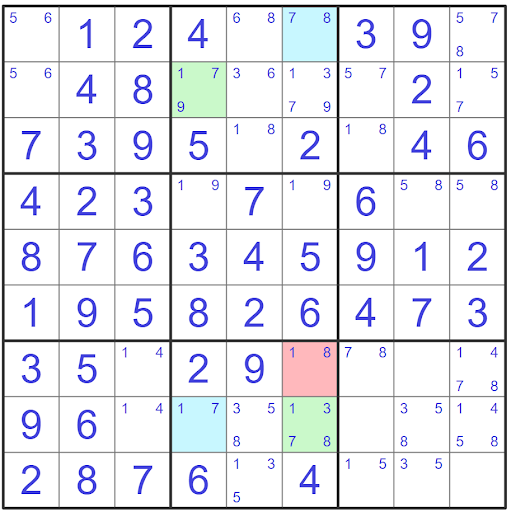
In this example using the XY-wing would allow us to eliminate two 7’s from each of the highlighted green cells as these cells both see the wings and do not already have their cell filled in with a value.

You’ve now learned how to solve the xy-wing. Put your skills to the test and see if you can find the xy-wing in a real Sudoku game.

Prerequisites

Before learning the XY-Wing, you should be comfortable with:

• Candidate notation (pencil marks) — complete candidates in every cell
• Naked singles and hidden singles — foundational solving
• Naked pairs and hidden pairs — subset elimination
• X-Wing — another advanced pattern technique

XY-Wing vs. Related Wing Techniques

Common Mistakes to Avoid

1. Pivot doesn’t see both pincers. The pivot must share a house (row, column, or box) with EACH pincer. The pincers don’t need to see each other.

2. Wrong candidate matching. The pivot (XY) must share X with one pincer and Y with the other. The pincers share Z — the candidate being eliminated.

3. Eliminating the wrong candidate. Only the SHARED candidate Z (common to both pincers) can be eliminated. Don’t eliminate X or Y.

4. Eliminating from cells that don’t see both pincers. The elimination only applies to cells in the intersection of both pincers’ visibility — cells that share a house with BOTH pincers.

5. Confusing with XYZ-Wing. If the pivot has three candidates instead of two, it’s an XYZ-Wing, which uses different elimination logic.

When to Look for XY-Wings

The XY-Wing is an advanced technique — use it after exhausting:

• All naked singles and hidden singles
• Naked pairs and hidden pairs
• Pointing pairs and pointing triples
• Naked triples and hidden triples
• X-Wings and Swordfish

XY-Wings appear in Expert and Evil difficulty puzzles. On SudokuPulse, Evil puzzles average about 3 XY-Wing applications per solve.

Frequently Asked Questions

Is an XY-Wing the same as a Y-Wing?

Yes. The terms are interchangeable. “Y-Wing” is the older name; “XY-Wing” is more descriptive because the pivot cell contains candidates X and Y.

How do I find the pivot?

Look for bivalue cells (cells with exactly two candidates). For each bivalue cell, check if two other bivalue cells in its houses have the right candidate pattern: one shares X, the other shares Y, and both contain Z.

Can an XY-Wing eliminate more than one candidate?

Each XY-Wing application removes one candidate (Z) from cells seeing both pincers. However, this often triggers new singles or enables other techniques.

What if no XY-Wing exists?

Try XYZ-Wings, W-Wings, Unique Rectangles, or Simple Coloring. Multiple advanced techniques may be needed for Evil puzzles.