X-Wing Sudoku Strategy
Today we will learn about the X-Wing technique and how we can sport and apply it to Sudoku puzzles. The X-Wing strategy will be useful in solving higher difficulty level Sudoku puzzles. This strategy will allow you to eliminate possible candidates from other cells.
Although this strategy is called “X-Wing” the patterns used are a part of the “Fish” types of Sudoku solving patterns. This is an important distinction to make as learning this pattern will also apply to the Swordfish and Jellyfish solving strategies.
The simplest explanation of this strategy is as follows:
The X-Wing strategy is a single-digit pattern that is made up of two parallel conjugate pairs.
It is very important that you understand what a conjugate pair is is. Let’s break it down: A conjugate pair refers to two cells that are within the same house (row, column or box) which are the only two cells that contain a specific candidate number.
For the purposes of a X-Wing a conjugate pair can only appear in a house that is a row or column not a block.
If this technical explanation was enough, play a real Sudoku game and try spotting a X-Wing.
If not, let’s take a look at the below Sudoku example to visualize this pattern:
Since this is a single digit pattern we will start off by looking at a Sudoku grid that only contains the candidates for a single number to help reduce the noise and highlight the X-Wing pattern easier.
Filtering a candidate by color is a great way to look for parallel conjugate pairs.
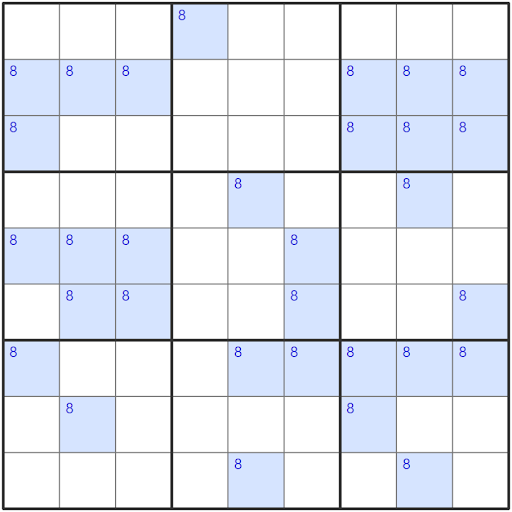
We can start scanning for conjugate pairs. For the purpose of the X-Wing the conjugate pair can only be in a house that is a column or row (not a block).
With all of the candidates filtered by color we can see that there are no columns that contain conjugate pairs and there are three rows (four, eight and nine) that have conjugate pairs. We can then see that rows four and nine are parallel to each other. Since these conjugate pairs are parallel to each other, we have successfully found an X-Wing.
The base sets for this X-Wing will be formed by the conjugate pairs in rows four and nine. While the cover sets will be perpendicular to the base sets intersecting with the candidates in r4c5, r4c8, r9c5, r9c8.
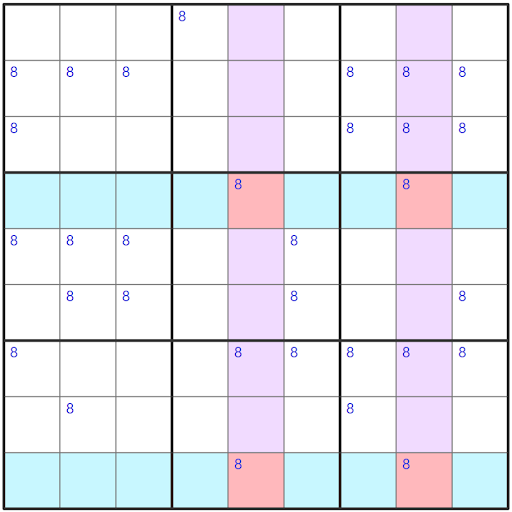
We can see that the base sets are highlighted in blue in rows four and nine. The cover sets are highlighted in purple on column five and eight.
For this to be a valid X-Wing the cover sets have to cover or intersect with the candidates of the conjugate pair.
All of the candidates in the cover sets except for those that intersect with the base set can then be eliminated (all of the purple shaded cells). This means that a X-Wing can eliminate up to fourteen candidates in total.
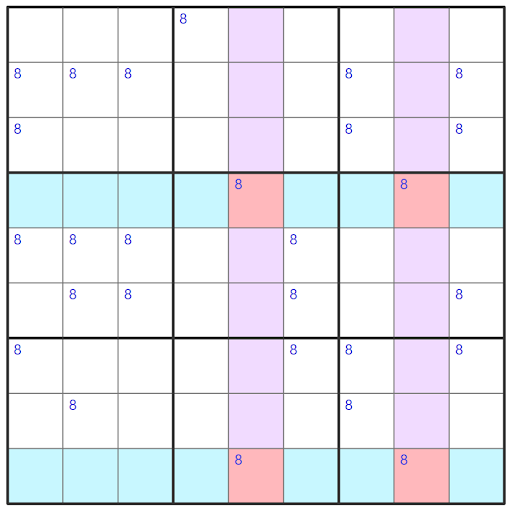
We were able to eliminate four candidates in this puzzle using the X-Wing technique.
Let’s take a look at another example.
Once again we start by highlighting all of one candidate to help us easily identify conjugate pairs. Starting with the rows we have conjugate pairs in rows one, two, five and seven. However, none of these pairs are parallel with each other. Looking at the columns we have conjugate pairs in column one, five and eight.
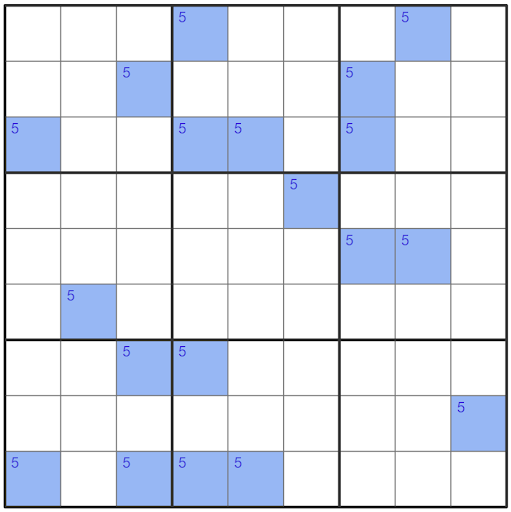
The conjugate pairs in columns one and five are parallel to each other. This means that we have successfully found our base sets for our X-Wing.
The base sets for this X-Wing will be formed by the conjugate pairs in columns one and five. While the cover sets will be perpendicular to the base sets intersecting with the candidates in r3c1, r9c1, r3c5, r9c5.
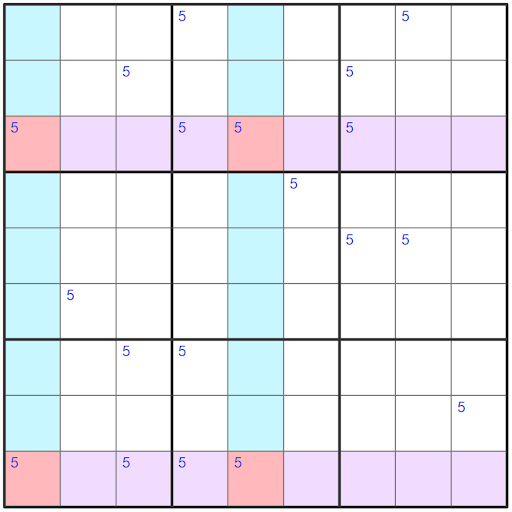
The base sets are now columns which are columns one and five highlighted in blue. With the cover sets intersecting these conjugate pairs in rows three and nine highlighted in purple.
A valid X-Wing has the cover sets intersecting with the conjugate pair in the base sets, which they do as shown by the red highlighted cells.
We can go ahead and remove the candidates from the cover sets which are the purple rows.
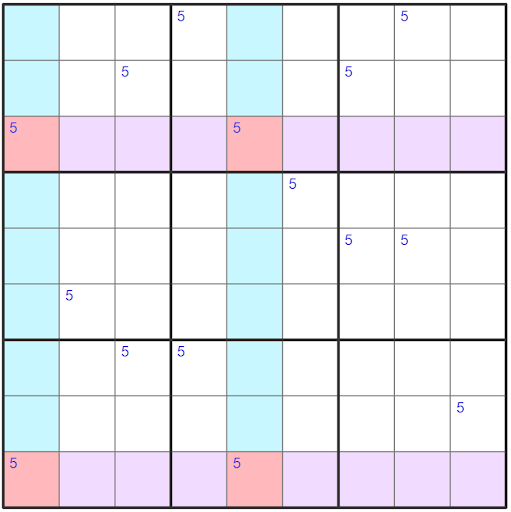
We were able to eliminate a total of our candidates from the cover sets in this example.
Logic of the X-Wing
Let’s work through an example of why this pattern works, which is also the reason this strategy is called an X-Wing. We will continue to use the above board where we have already determined that the base sets are columns one and five and the candidate needs to go in r3c1, r3c5, r9c1 or r9c5.
Since each candidate can only appear once in each base set, for column one that means that the candidate is either in row three or nine. Let’s assume that the candidate is in row three. This means that the candidate in the column five base set would have to be in row nine.
If there is a candidate in r3c1 the only other spot in the X-Wing which is not in the same house or does not see the candidate is diagonal in the X-Wing. It is this diagonal pattern that creates an X which is the reason this strategy is called an X-Wing.
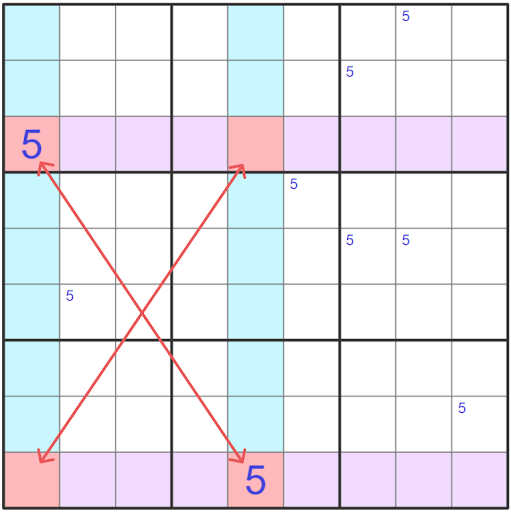
There are also a couple of other ways to spot and understand this pattern if you are familiar with the Alternate Interest Chain Type 1 or continuous loops.
Understanding the X-Wing as a AIC (Alternating Inference Chain) Type 1 or Continuous Loop
An X-Wing also follows the same pattern as an AIC Type 1, when we remember that a house is still only a column or row.
An AIC Type 1 has the following link pattern strong-weak-strong where it both starts and ends on a strong link. This means that one of the digits has to be placed in one of the end cells of the AIC which eliminates that digit from all cells that can see both ends of the AIC.
The chain is started by assuming a candidate is false and one of the two ends of the chain will always be true. This means that we are able to eliminate all of the candidates that see both of the chain’s ends.
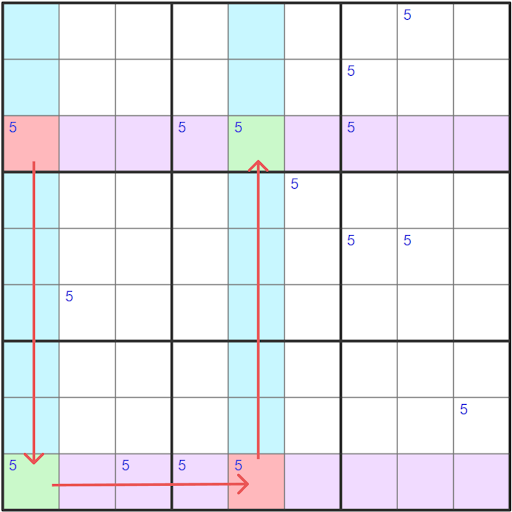
Our AIC chain starts in r3c1 (false, red) which is a strong link to r9c1 (true, green) since this is a conjugate pair. The next link is weak since there are many other candidates in row nine as we move from r9c1 (true, green) to r9,c5 (false, red). Our last link is between our other conjugate pair which makes it a strong link as we move from r9c5 (false, red) to r3c5 (true, green).
Since one of the ends of this chain has to be true, either r3c1 or r3c5 that means that all other candidates in row three can be eliminated.
We will now repeat this process, in the opposite direction.
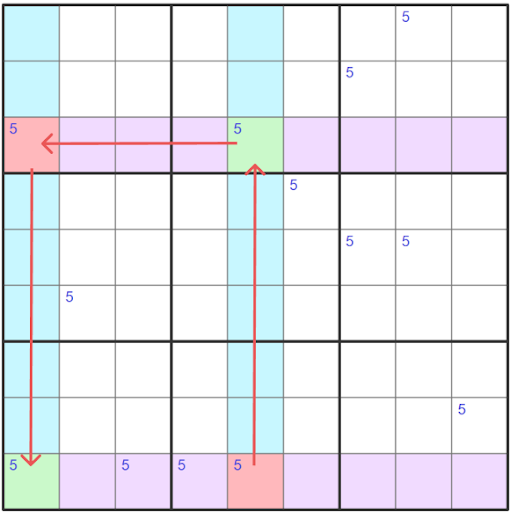
Since our AIC Type 1 chain now ends in row nine. We are able to eliminate all other candidates in row nine that are not at the ends of this chain. This provides us with the same outcome as eliminating all of the candidates in our cover sets that don’t intersect with the base sets.
This same example can also be demonstrated as a continuous loop where the connection between the chain is strong-weak-strong-weak and completes the loop. This also shows us that the correct answer must be the two diagonals that were highlighted in the X-Wing breakdown.
You’ve now learned how to solve the x-wing. Put your skills to the test and see if you can find the x-wing in a real Sudoku game.