XYZ-Wing Sudoku Strategy
The XYZ-wing strategy is a complex Sudoku technique that can be used to help eliminate candidates and solve hard Sudoku puzzles. The XYZ-wing strategy belongs to the “wing” family as it involves a pivot and two pincers similar to techniques such as the XY-wing.
What is an XYZ-wing
An XYZ-wing involves three candidates as its name implies. Instead of using XYZ we will use the letters ABC to explain this strategy.
The XYZ-wing is a pattern where a pivot cell which contains all three candidates (ABC) and is in the same house as the two wings. The two wings (also known as pincers) are conjugate pairs that contain the same candidates as those in the pivot cell with different groupings from each other. The last criteria is that one of the pincers needs to be in the same block as the pivot cell.
How to spot an XYZ-wing
Let’s go over an example to understand how to spot this pattern better. We will then break down some steps that you can follow which will make finding XYZ-wings much faster to avoid needing to go through the process of finding a pivot and two pincers before checking if a successful XYZ-wing will allow you to eliminate candidates.
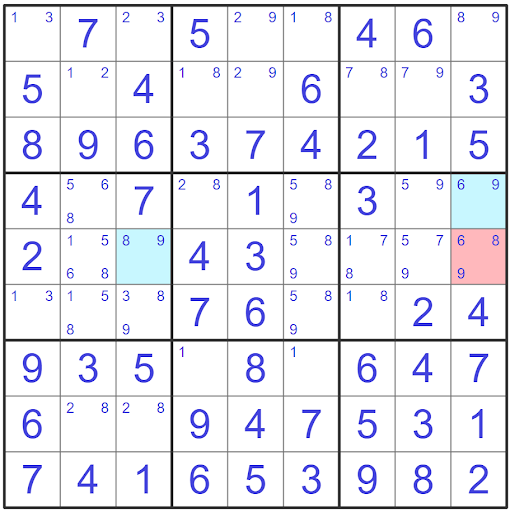
The above example shows a XYZ-wing with the pivot cell shaded in red and the two pincers shaded in blue.
To spot this pattern we can first start off by looking for bi-value cells within each block which will act as our first pincer. The first pincer that we have is in r4c9 and has the candidates (69).
Since the pivot cell has to be in the same block as one of the pincers we can start looking for a cell that has three candidates, two of which match the candidates in the first bi-value cell that we found. We can see that the cell in r5c9 matches this criteria as it contains candidates (689).
The last pincer that we find will need to be in the same house as the pivot as well as have two candidates while being a different grouping from the other pincer. Since grouping (69) is used by the first pincer the second pincer will need to be either (68) or (89) to follow the pattern of the XYZ-wing.
After scanning r5 and c9 which are in the same house as the pivot we find our other pincer in row r5c3 with a bi-value of (89). If you have been scanning the puzzle you may be wondering if we can use cell r1c9 as it also contains candidates (89) and is in the same house as the pivot.
This cell would not be valid as it would mean all three of the cells would be in the same house. If it is the case where all three cells were contained in the same house we would have a naked triple.
XYZ-wing candidate elimination example
Now that we have successfully identified a XYZ-wing, let’s go over how we can go about eliminating candidates to help us solve this puzzle.
Since the first pincer is in the same block as the pivot, we are able to eliminate candidates from cells that intersect with the pivot and the second pincer.
Since we are able to eliminate the candidates present in the XYZ-wing that intersect with the pivot and the second pincer (the pincer/wing outside of the block the pivot is present in) we can remove the candidates C from the cells that are shaded in purple. Since candidate C is the shared candidate between the two pincers this means that we can remove 9 from any of the purple shaded cells. This means that we would be able to remove a 9 from cell r5c8.
Best way to find XYZ-wings
There is a good process to follow that will help you find XYZ-wings and save time doing so.
The first step is looking in each block for a bi-value cell as this will act as the first wing. Once you have found a bi-value cell you should look within the block to see if there is a cell with exactly three candidates two of which are contained in the first block.
If there is no cell that follows this criteria there is no XYZ-wing and you should restart this process with a different bi-value cell. If there is a cell that matches this criteria you should then check to see its position in the block relative to the pivot cell.
If the pivot cell is in the same row as the first pincer, this means that the second pincer will be in the same column as the pivot. Conversely, if the pivot cell is in the same column as the first pincer, the second pincer will be in the same row as the pivot.
This shortcut works because the pivot must share a house (row, column, or box) with each pincer, and one pincer is already in the same box. The second pincer must connect to the pivot through a different house — either the same row or the same column.
Once you know where to look for the second pincer, check if there is a bi-value cell with the correct candidate pair. If so, verify that the shared candidate (the one common to both pincers) can be eliminated from cells that see all three XYZ-wing cells.
XYZ-Wing vs. Naked Triple
At first glance, an XYZ-wing looks similar to a naked triple. The key difference is:
| Feature | Naked Triple | XYZ-Wing |
|---|---|---|
| Location | All three cells in the same house | Cells span different houses |
| Effect | Eliminates candidates from the shared house | Eliminates from cells that see all three cells |
| Candidates | Three values across three cells | Pivot has 3 candidates; pincers each have 2 |
If all three cells are in the same row, column, or box, you have a naked triple — not an XYZ-wing. The XYZ-wing specifically requires the cells to be in different houses so that the elimination logic applies to the intersection of their visibility.
Common Mistakes to Avoid
Confusing XYZ-Wing with a naked triple. If all three cells are in the same house, it’s a naked triple. The XYZ-wing requires the cells to span different houses.
Forgetting the box constraint. One pincer must be in the same box as the pivot. If both pincers are outside the pivot’s box, the pattern doesn’t work as an XYZ-wing.
Eliminating the wrong candidate. Only the candidate shared by both pincers (Z) can be eliminated, and only from cells that can see all three XYZ-wing cells simultaneously.
Incomplete pencil marks. Like all advanced techniques, XYZ-wings are invisible without accurate and complete candidate notation.
Missing the elimination zone. The elimination only applies to cells that see all three cells of the XYZ-wing — not just cells that see the pivot.
When to Look for an XYZ-Wing
The XYZ-wing is an advanced technique. Don’t start looking for it until you’ve exhausted:
- All naked singles and hidden singles
- Naked pairs and hidden pairs
- Pointing pairs and pointing triples
- Naked triples and hidden triples
- X-Wings and Swordfish
- XY-Wings
XYZ-wings most commonly appear in Expert and Evil difficulty puzzles.
Frequently Asked Questions
How is an XYZ-Wing different from an XY-Wing?
The XY-Wing has a pivot with two candidates and two pincers with two candidates each. The XYZ-Wing has a pivot with three candidates and two pincers with two candidates each. In an XY-Wing, the pivot doesn’t contain the candidate being eliminated, while in an XYZ-Wing it does — which means the elimination zone is more restricted (only cells seeing all three cells).
Can an XYZ-Wing eliminate more than one candidate at a time?
No. An XYZ-wing targets exactly one candidate — the value shared by both pincers. However, removing that candidate may trigger cascading eliminations through simpler techniques.
How rare is the XYZ-Wing?
XYZ-Wings appear primarily in Expert and Evil difficulty puzzles. They’re less common than XY-Wings but more common than techniques like chains or ALS. On SudokuPulse, Evil puzzles average about 2 XYZ-Wing applications per solve.
What if I can’t find any XYZ-Wings?
If you’ve checked for XYZ-Wings and found none, the puzzle may require other advanced techniques like Unique Rectangles, W-Wings, coloring, or chains. Verify your pencil marks are complete and try scanning from different angles.
Practice the XYZ-Wing
Put the XYZ-wing into practice and test if you can find the XYZ-wing in a real Sudoku game. Try our Expert or Evil difficulty puzzles.
Practice XYZ-Wing Sudoku Strategy
Ready to apply what you've learned? Practice this technique with interactive puzzles designed to reinforce your skills.
Practice Now →