Naked Pair (Conjugate Pair) Sudoku Strategy
Naked pairs are also commonly referred to as conjugate pairs and are a good Sudoku strategy that can be applied to help solve Sudoku puzzles.
While the strategy is simple, conjugate pairs form the base for many advanced techniques such as the x-wing and xy-wing. However, this strategy is still powerful on its own as finding conjugate pairs can help eliminate many candidates from the grid.
What is a conjugate pair?
A conjugate pair is present when there is a set of two candidate numbers between exactly two cells which belong to the same house.
How to spot a naked pair (conjugate pair)
We can spot a naked pair by scanning the Sudoku grid for cells that only contain two possible candidates. We can then check each cell that has only two candidates to see if there is another cell within the same house (row, column or block) that also only has these two candidates. Take a look at the example example below:
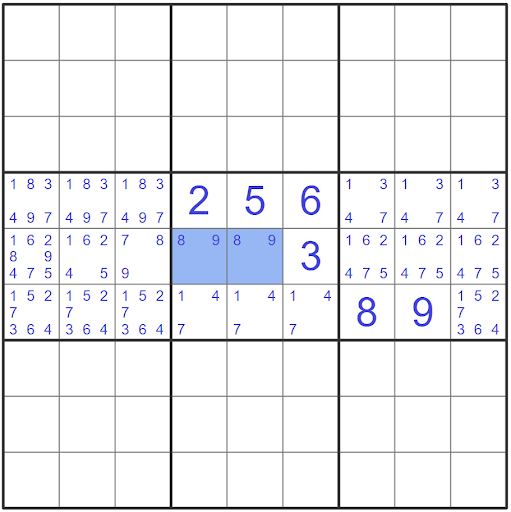
We can spot the naked pair in the blue highlighted cells r5c4 and r5c6 which both have the candidates (89). Since there are exactly two cells with the two same candidates, this satisfied the first portion of a conjugate pair. Next, we need to confirm that this pair of cells are in the same house, which they are as they both share block 5. We can confirm that we have found a conjugate pair.
Sometimes naked pairs can be hidden which are also referred to as hidden pairs. This happens when the cell has additional markings which make the cell appear to have more options when it actually only has a pair.
Now that we know how to identify and find a naked pair, we can move onto how we are able to eliminate candidates to help us solve this puzzle.
Naked pair (conjugate pair) example
Let’s go over an example of how to eliminate candidates once you have found a conjugate pair.
Once the naked pair has been identified, we know that the two candidates must be present in one of the two cells. This means that any other cells that overlap with this conjugate pair can not be the two candidates present. This allows us to eliminate these two candidates from the cells highlighted in red.
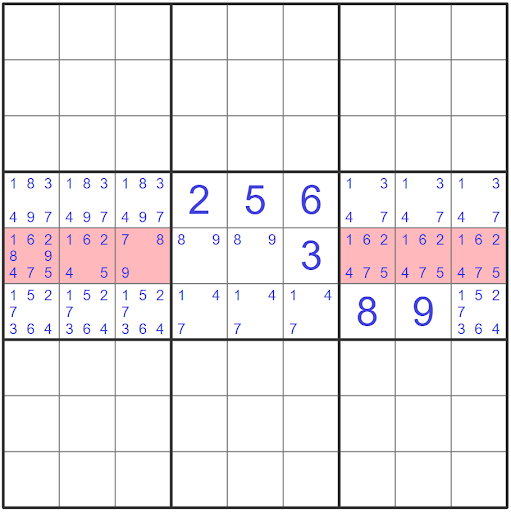
We will be able to eliminate all of the candidates (89) from row 5 in this case. You will notice that the cells in block five are not highlighted red even though they share a house. This is because if they were any of these candidates (89) in block 5 we would not have a conjugate pair present.
Let’s take a look at another example to make sure you know how to spot a naked pair and eliminate the correct candidates.
We will start by highlighting all of the cells with two candidates in blue to help us identify connections between them.
We can then start scanning to see if there are any other cells within the same house that also contain the same two candidates.
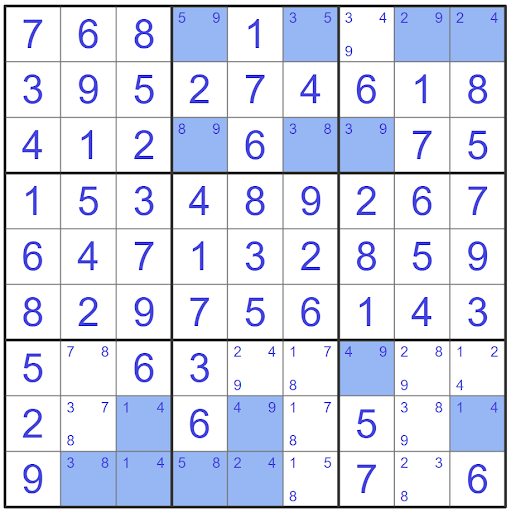
In the case of this example the conjugate pair is between cells r8c3 and r8c9. These are exactly two cells that share the same house (row 8) which both have the same two candidates (14).
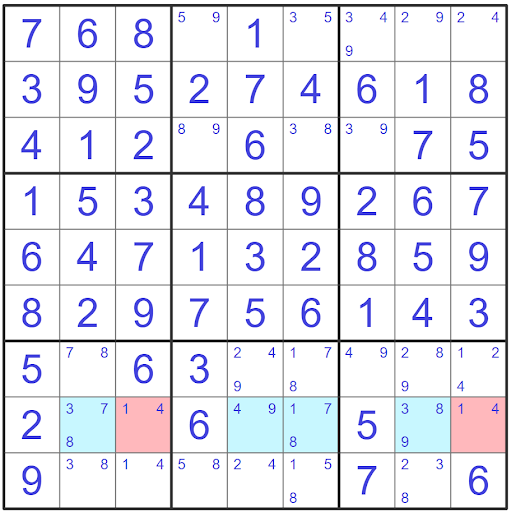
This will allow us to eliminate candidates (14) from all of the shaded blue cells. The conjugate pair technique has allowed us to eliminate a total of two candidates. The 4 from cell r9c5 and the 1 from cell r8c6. With the elimination of the 4 in cell r8c8 we are now able to solve that cell for the value of 9!
You may have identified the (49) pair in r7c7 and r8c5 as these are exactly two cells that contain the same two candidates. However, these two cells do not satisfy the rule that they must be in the same house (row, column, block). We can see this by breaking down the houses that these two cells belong to:
| House | cell r7c7 | cell r8c5 | match? |
|---|---|---|---|
| Row | 7 | 8 | No |
| Column | 7 | 5 | No |
| Block | 8 | 9 | No |
There is actually another conjugate pair in this puzzle between the candidates (14) in r8c3 and r9c3. These are exactly two cells that share the same two candidates and are in the same house (block 7). However, since they would be able to eliminate candidates (14) from column 3 that is already filled in with values, it is not helpful to us.
You’ve now learned how to spot a naked pair and use this strategy to eliminate candidates. Put your skills to the test and use this technique in a real Sudoku game.